Research Projects

Doubly Mixed-Effect Gaussian Process Regression (DMGP)

Doubly mixed-effects GP (left) and translated mixed-effects GP (right)

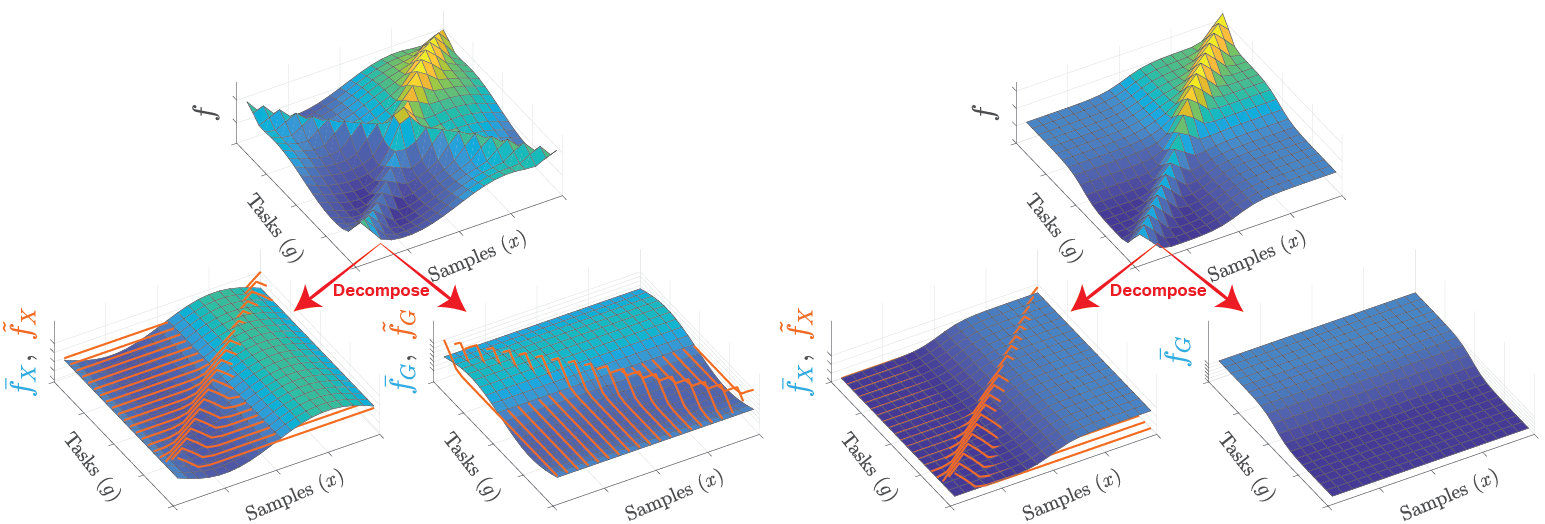
We address the problem of multi-task regression with Gaussian processes (GPs) with the goal of obtaining a decomposition of input effects on outputs into components shared across or specific to tasks and samples. We propose a family of mixed-effects GPs, including doubly and translated mixed-effects GPs, that performs such a decomposition, while also modeling the complex task relationships. Instead of the tensor product widely used in multi-task GPs, we use the direct sum and Kronecker sum for Cartesian product to combine task and sample covariance functions. With this kernel, the overall input effects on outputs decompose into four components: fixed effects shared across tasks and across samples and random effects specific to each task and to each sample. We describe an efficient stochastic variational inference method for our proposed models that also significantly reduces the cost of inference for the existing mixed-effects GPs. On simulated and real-world data, we demonstrate higher test accuracy and interpretable decomposition from our approach.

• Doubly Mixed-Effects Gaussian Process Regression
  Jun Ho Yoon, Daniel P. Jeong, Seyoung Kim.
  Proceedings of the 25th International Conference on Artificial Intelligence and Statistics (AISTATS), PMLR 151:6893-6908, 2022.
  Accepted for oral presentation (2.6% of submitted papers).
  [paper, software]

Eigen Graphical Lasso (EiGLasso)

Kronecker sum (left) vs. Kronecker product (right).

In many real-world data, complex dependencies are present both among samples and among features. The Kronecker sum or the Cartesian product of two graphs, each modeling dependencies across features and across samples, has been used as an inverse covariance matrix for a matrix-variate Gaussian distribution, as an alternative to Kronecker-product inverse covariance matrix due to its more intuitive sparse structure. However, the existing methods for sparse Kronecker-sum inverse covariance estimation are limited in that they do not scale to more than a few hundred features and samples and that the unidentifiable parameters pose challenges in estimation. In this paper, we introduce EiGLasso, a highly scalable method for sparse Kronecker-sum inverse covariance estimation, based on Newton’s method combined with eigendecomposition of the sample and feature graphs to exploit the Kronecker-sum structure. EiGLasso further reduces computation time by approximating the Hessian matrix based on the eigendecomposition of the two graphs. EiGLasso achieves quadratic convergence with the exact Hessian and linear convergence with the approximate Hessian. We describe a simple new approach to estimating the unidentifiable parameters that generalizes the existing methods. On simulated and real-world data, we demonstrate that EiGLasso achieves two to three orders-of-magnitude speed-up, compared to the existing methods.

Collapsing the sprase Kronecker-sum structure to compute gradients.

• EiGLasso for Scalable Sparse Kronecker-Sum Inverse Covariance Estimation
  Jun Ho Yoon, Seyoung Kim.
  Journal of Machine Learning Research, 23(110):1−39, 2022.
  [paper, software]
• EiGLasso: Scalable Estimation of Cartesian Product of Sparse Inverse Covariance Matrices
  Jun Ho Yoon, Seyoung Kim.
  Proceedings of the 36th Conference on Uncertainty in Artificial Intelligence (UAI), PMLR 124:1248-1257, 2020.
  [paper, talk, software]